Shape factors
On this page
Calculations of driving forces, interfacial compositions and growth rates were previously shown for spherical precipitates, in which the radius of curvature is constant across the surface. For non-spherical precipitates, the curvature varies.
While it is possible to model a single precipitate to investigate the thermodynamic and kinetic behavior across the surface, this is impractical for the KWN model. Rather, a correction factor is applied to the thermodynamic and kinetic terms.
In defining the precipitate shape, three terms will be used: the long axis ($l$), the short axis ($r$) and the equivalent spherical radius ($R$). Additionally, for ellipsoids, the eccentricity can be defined (which simplifies some of the following equations). The equivalent spherical radius is defined as the radius of a sphere that gives the same volume as the non-spherical precipitate. Defining the precipitate size by the equivalent radius minimizes the amount of changes needed to the KWN model (such as calculating volume fraction and composition).
$$ \alpha = \frac{l}{r} $$
$$ e = \sqrt{1 - \frac{1}{\alpha^2}} $$
The changes made to the growth rate and Gibbs-Thomson effect are then:
$$ \frac{dR}{dt} = f(\alpha) \frac{dR}{dt} \biggr\rvert_{sphere} $$
$$ \mu_A^\alpha = \mu_A^\beta + \left(g(\alpha) \frac{2\gamma}{R} + \Delta G_{el} \right) V_M^\beta $$
Sphere
The equations for a spherical precipitate reduces the KWN model to its original equations.
$$ R_{eq} = r $$
$$ f(\alpha) = 1 $$
$$ g(\alpha) = 1 $$

Spherical precipitate shape
Needle
$$ R_{eq} = r \sqrt[3]{\alpha} $$
$$ f(\alpha) = \frac{2 e \sqrt[3]{\alpha^2}}{\ln{(1+e)} - \ln{(1-e)}} $$
$$ g(\alpha) = \frac{1}{2 \sqrt[3]{\alpha^2}} \left(1 + \frac{\alpha}{e} \sin^{-1}{e} \right) $$
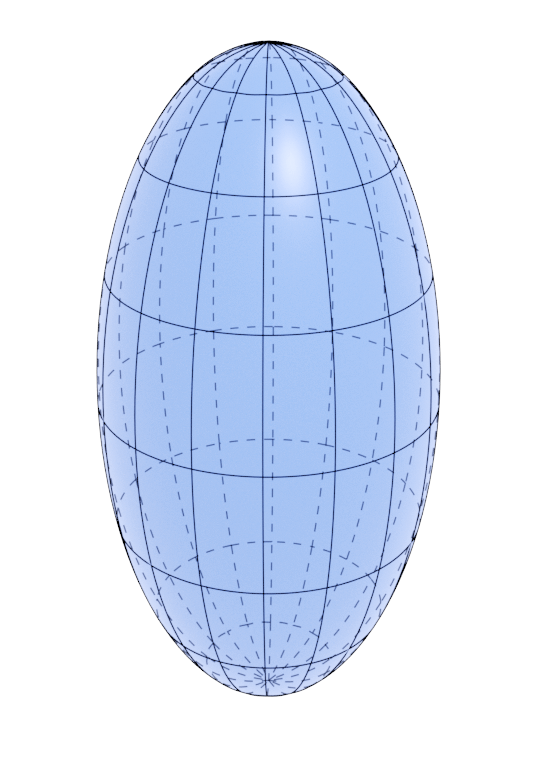
Needle-like precipitate shape
Plate
$$ R_{eq} = r \sqrt[3]{\alpha^2} $$
$$ f(\alpha) = \frac{e \sqrt[3]{\alpha^2}}{\pi/2 - \cos^{-1}{e}} $$
$$ g(\alpha) = \frac{1}{2 \sqrt[3]{\alpha^4}} \left(\alpha^2 + \frac{1}{2 e} \ln{ \left(\frac{1+e}{1-e} \right)} \right) $$
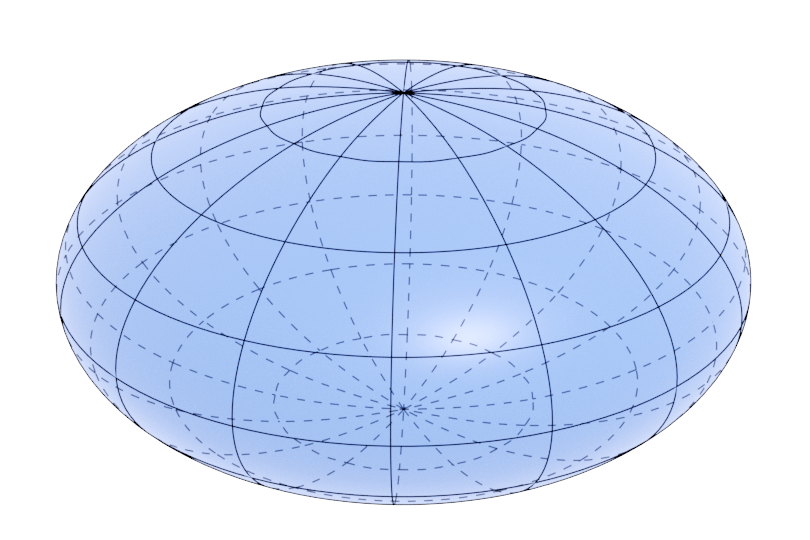
Plate-like precipitate shape
Cuboid
$$ R_{eq} = \sqrt[3]{\frac{3\alpha}{4\pi}} l $$
$$ f(\alpha) = 0.1 \exp{ \left(-0.091 (\alpha-1)\right)} + \frac{1.736 \sqrt{\alpha^2 - 1}}{\sqrt[3]{\alpha} \ln{ \left( 2\alpha^2 + 2\alpha \sqrt{\alpha^2 - 1} - 1 \right)}} $$
$$ g(\alpha) = \frac{2\alpha + 1}{2\pi} \left( \frac{4 \pi}{3 \alpha} \right)^{2/3} $$
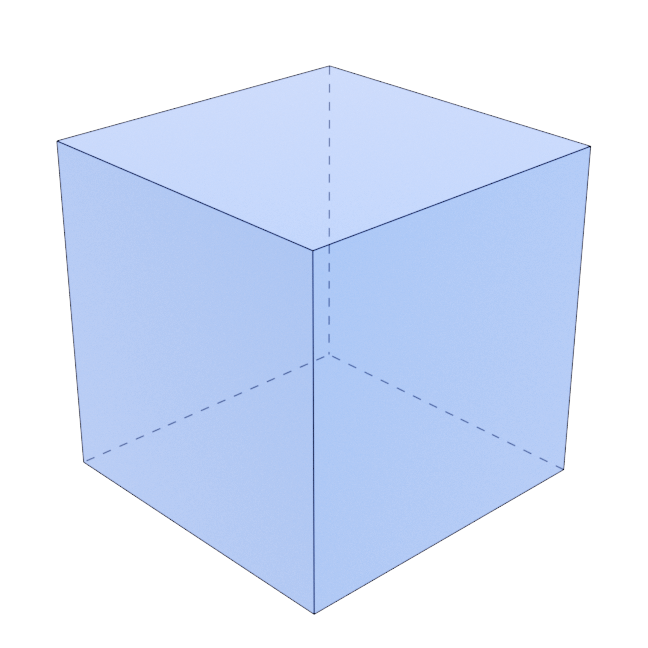
Cuboidal precipitate shape
References
K. Wu, Q. Chen and P. Mason, “Simulation of precipitation kinetics with non-spherical particles” Journal of Phase Equilibria and Diffusion 39 (2018) p. 571
B. Holmedal, E. Osmundsen and Q. Du, “Precipitation of non-spherical particles in aluminum alloys Part I: Generalization of the Kampmann-Wagner numerical model” Metallurgical and Materials Transactions A 47A (2016) p. 581