Grain Boundary Factors
For precipitates that nucleate on grain boundaries, the number of available nucleation sites, the nucleation barrier and the precipitate morphology will differ from bulk nucleation. Grain boundary nucleation can be divided into three types: two-grain junctions (grain boundaries), three-grain junctions (grain edges) and four-grain junctions (grain corners).
Nucleation on a grain boundary requires both the formation of a precipitate-matrix interface and the removal of a grain boundary area (matrix-matrix interface). The Gibbs free energy involved in nucleating a precipitate is thus
$$ \Delta G = -c R^3 \Delta G_{v} + b \gamma_{\alpha \beta} R^2 - a \gamma_{\alpha \alpha} R^2 $$
Where $\gamma_{\alpha \alpha}$ is the grain boundary energy and $\gamma_{\alpha \beta}$ is the interfacial energy between the precipitate and the matrix. $R$ is the radius of curvature. $a, b, \text{ and } c$ are multiplying factors to the radius to obtain the grain boundary area that is removed, the surface area of the precipitate and the volume of the precipitate.
This difference in the Gibbs free energy for nucleation changes the height of the nucleation barrier and the critical radius.
$$ \Delta G^{*} = \frac{4}{27} \frac{\left(b \gamma_{\alpha \beta} - a \gamma_{\alpha \alpha}\right)^3}{c^2 {\Delta G_{v}}^2} $$
$$ R^{*} = \frac{2 \left(b \gamma_{\alpha \beta} - a \gamma_{\alpha \alpha}\right)}{3 c \Delta G_{v}} $$
$a$, $b$ and $c$ for grain boundaries, edges and corners are easier defined by introducing a new term, $k$, which is the ratio between the grain boundary energy and the interfacial energy. This also represents the wetting angle between the grain boundary and precipitate-matrix interface.
$$ k = \cos{\theta} = \frac{\gamma_{\alpha \alpha}}{2 \gamma_{\alpha \beta}} $$
Note that in the limit that $\gamma_{\alpha \alpha} \rightarrow 0$, then $k \rightarrow 0$. When this occurs, the shape of the precipitate becomes spherical. Thus $b \rightarrow 4 \pi$ and $c \rightarrow \frac{4 \pi}{3} $.
While $a$ will be non-zero in this limit, the energy change in removing the grain boundary area will be zero (since $\gamma_{\alpha \alpha} = 0$). Thus, $ \Delta G^* $ and $ R^* $ will reduce to what is predicted by classical nucleation theory.
Dislocations
While dislocations are grain boundaries, the same equations can still be used (this is also true for bulk nucleation as well). Values for $a$, $b$ and $c$ are taken to reduce $ \Delta G^* $ and $ R^* $ to what is given by CNT. $a$ is 0 since there is no grain boundary will be removed during nucleation.
$$ a = 0 $$
$$ b = 4 \pi $$
$$ c = \frac{4 \pi}{3} $$
Two-grain junctions (Grain boundaries)
Larger values of $\gamma_{\alpha \alpha}$, and thus $k$, leads to smaller wetting angles. If the grain boundary energy is too large, there will be no nucleation barrier. In this case, precipitation will only be governed by the precipitate growth rate and the grain boundary area. For two-grain junctions, this occurs when $k \geq 1$.
$$ a = \pi \left(1 - k^2\right) $$
$$ b = 4 \pi \left(1 - k\right) $$
$$ c = \frac{2 \pi}{3} \left(2 - 3 k + k^2\right) $$
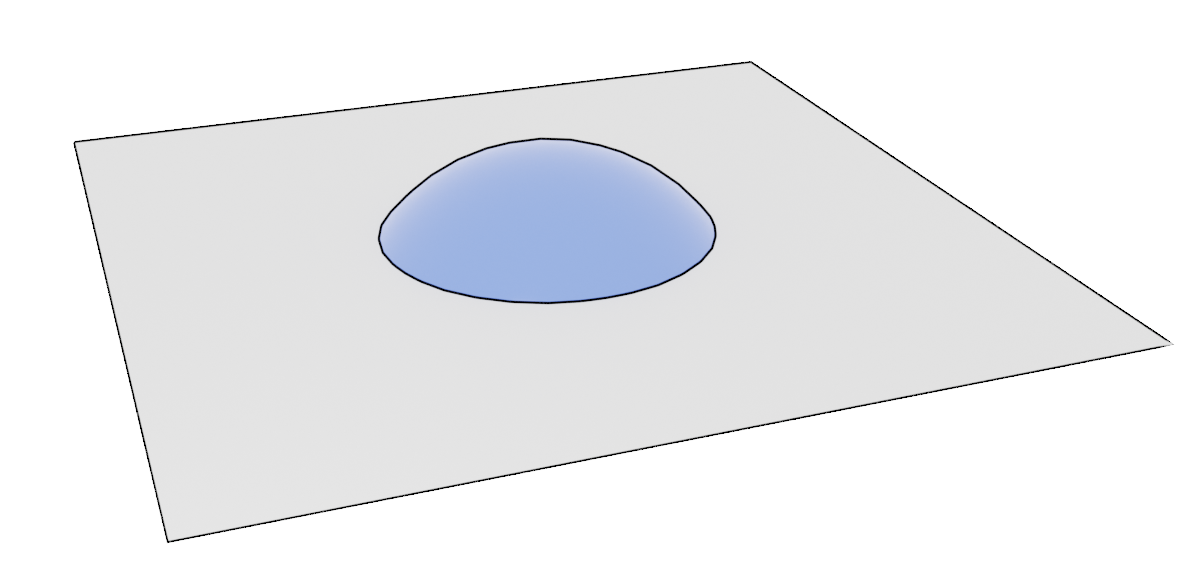
Precipitate shape on a grain boundary
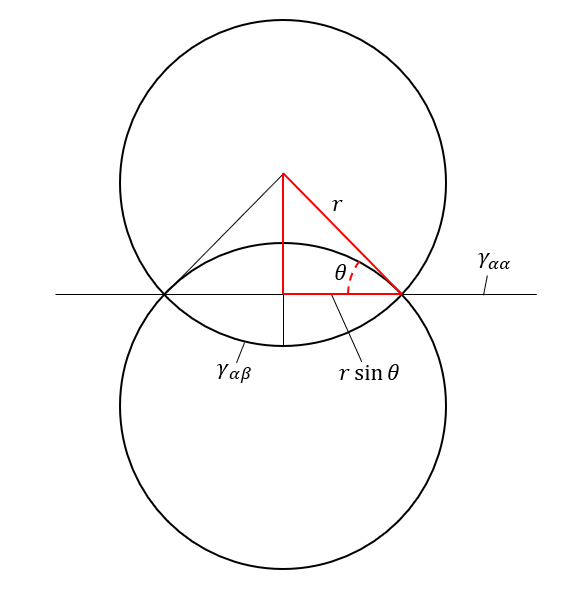
Cross section of grain boundary precipitate. The same concept applies to grain edges and corners.
Three-grain junctions (Grain edges)
For three-grain junctions, the nucleation barrier disappears when $k \geq \frac{\sqrt{3}}{2}$.
$$ a = 3 \beta \left(1 - k^2\right) - k \sqrt{3 - 4 k^2} $$
$$ b = 12 \left(\frac{\pi}{2} - \alpha - k \beta\right) $$
$$ c = 2 \left(\pi - 2\alpha + k^2 \sqrt{3 - 4 k^2} - \beta k \left(3 - k^2\right)\right) $$
Where
$$ \alpha = \sin^{-1}{\frac{1}{2 \sqrt{1 - k^2}}} $$
$$ \beta = \cos^{-1}{\frac{k}{\sqrt{3 \left(1 - k^2\right)}}} $$
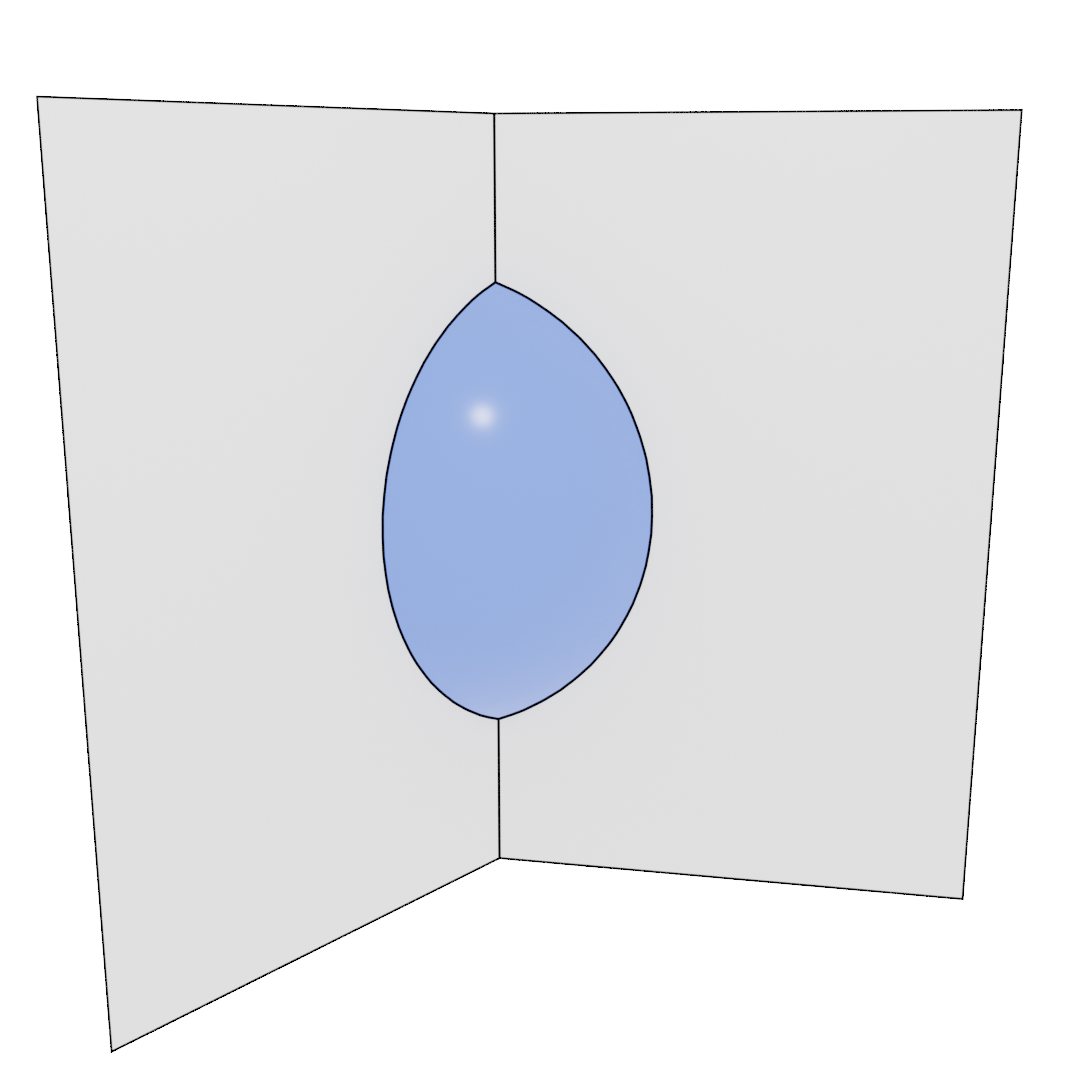
Precipitate shape on a grain edge
Four-grain junctions (Grain corners)
For four-grain junctions, the nucleation barrier disappears when $k \geq \sqrt{\frac{2}{3}}$.
$$ a = 3 \left(2 \phi \left(1 - k^2\right) - K \left(\sqrt{1 - k^2 - \frac{K^2}{4}} - \frac{K^2}{\sqrt{8}}\right)\right) $$
$$ b = 24 \left(\frac{\pi}{3} - k \phi - \delta\right) $$
$$ c = 2 \left(4 \left(\frac{\pi}{3} - \delta\right) + k K \left(\sqrt{1 - k^2 - \frac{K^2}{4}} - \frac{K^2}{\sqrt{8}}\right) - 2 k \phi \left(3 - k^2\right)\right) $$
Where
$$ K = \frac{4}{3} \sqrt{\frac{3}{2} - 2 k^2} - \frac{3}{2} k $$
$$ \phi = \sin^{-1}{\frac{K}{2 \sqrt{1 - k^2}}} $$
$$ \delta = \cos^{-1}{\frac{\sqrt{2} - k \sqrt{3 - K^2}}{K \sqrt{1 - k^2}}} $$
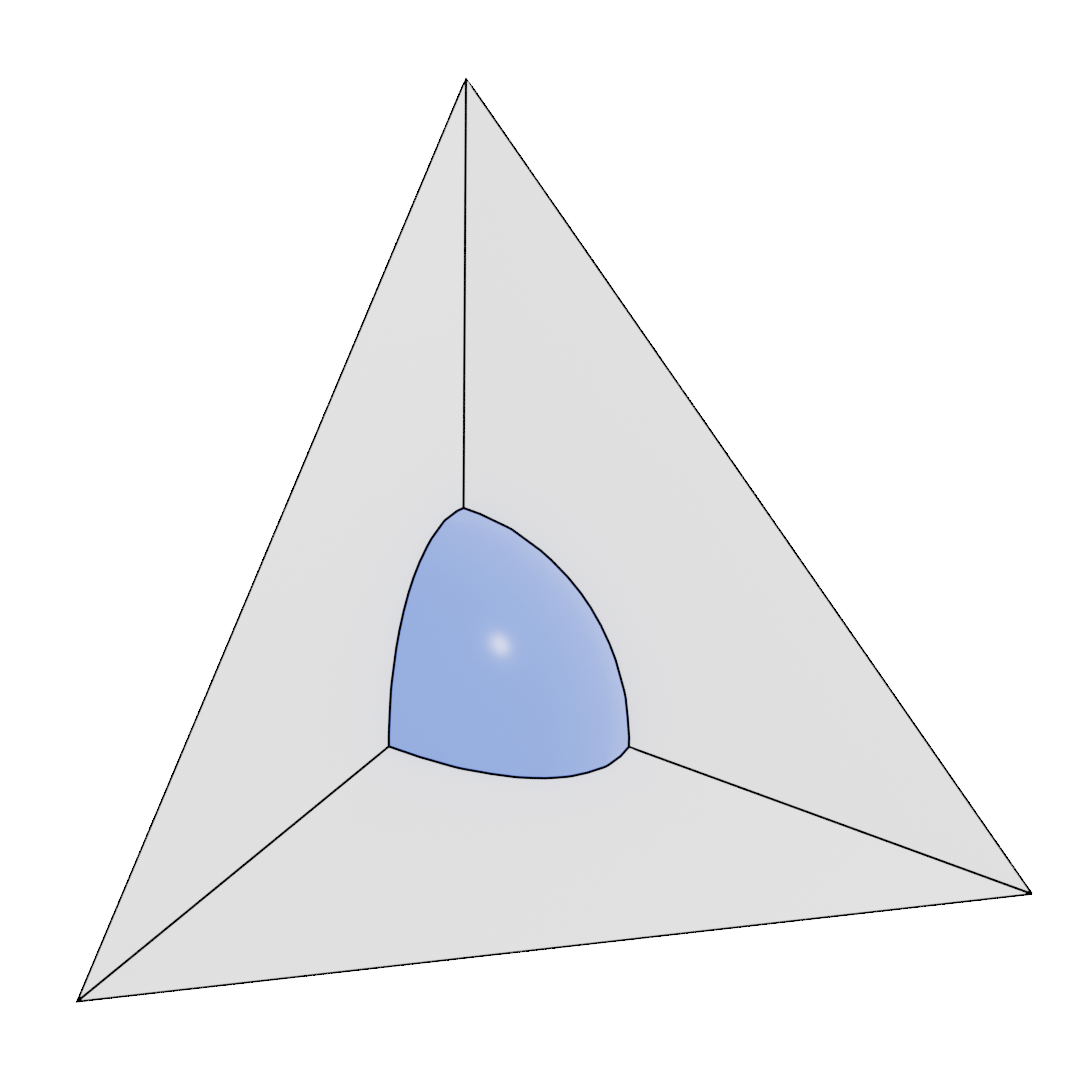
Precipitate shape on a grain corner
Nucleation sites
The nucleation site density ($N_0$) is determined by treating all lattice sites as potential nucleation sites. This is dependent on the density of lattice sites, $\rho_i$, where i represents the number of dimensions (0, 1 or 2).
$$ N_0 = \rho_i \left(\frac{N_A}{V_m^\alpha}\right)^{i/3} $$
For dislocations, the density is just the dislocation density. Since dislocations are line defects, the density of lattice sites is a linear density.
$$ \rho_1 = \rho_d $$
For grain boundaries, edges and corners, the lattice site density depends on the grain size (D) and aspect ratio (A). The grains are assumed to be in the shape of a tetrakaidecahedron.
$$ \text{Grain Boundaries } \quad\quad \rho_2 = \frac{6 \sqrt{1+2 A^2} + 1 + 2 A}{4 A D} $$
$$ \text{Grain Edges } \quad\quad \rho_1 = 2 \frac{\sqrt{2} + 2 \sqrt{1+A^2}}{A D^2} $$
$$ \text{Grain Corners } \quad\quad \rho_0 = \frac{12}{A D^3} $$
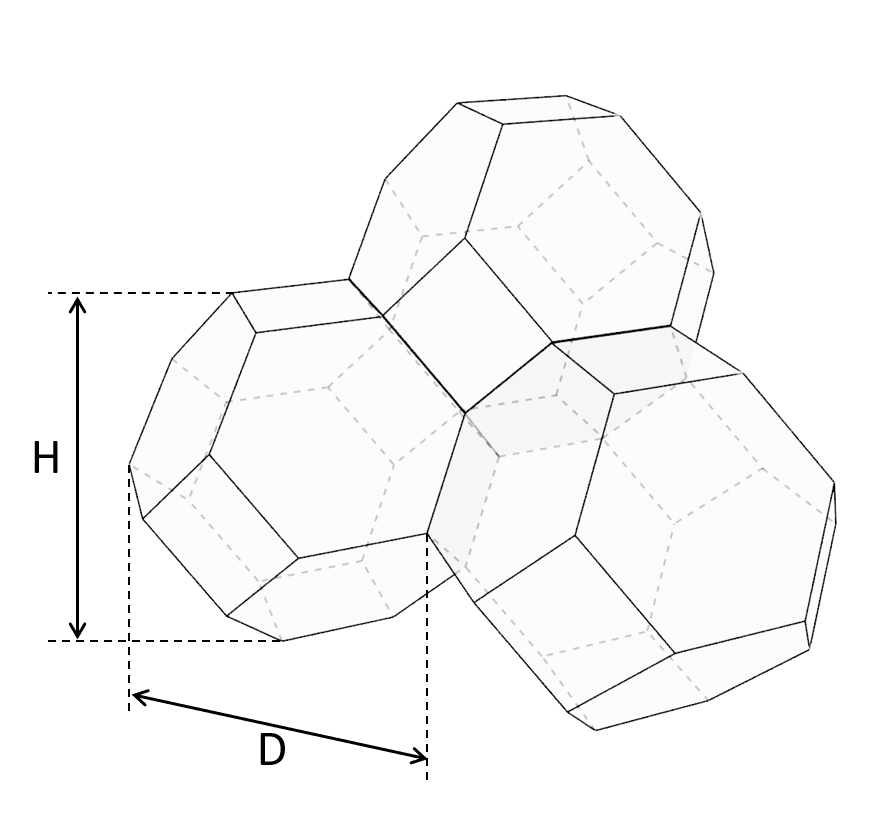
Shape of a grain
Other changes
The Zeldovich factor is modified by
$$ Z = Z_b \sqrt{\frac{3c}{4\pi}} $$
Where $Z_b$ is the Zeldovich factor for bulk nucleation.
The impingement rate becomes
$$ \beta = \frac{b}{4\pi} \beta_b $$
For outputting results, the average radius is stored as the radius of curvature. However, the plotted radius is related to the area of removed grain boundaries.
$$ r = \sqrt{\frac{a}{\pi}} R $$
References
- P. J. Clemm and J. C. Fisher, “The influence of grain boundaries on the nucleation of secondary phases” Acta Metallurgica 3 (1955) p. 70